You can find a static output feedback (SOF) gain calculator and a frequency domain shaped state feedback calculator in this site. Despite the html form based design is not user friendly, you can expect pretty good results from these solvers. First, let me very briefly give some background information on these solvers.
Static feedback
In the control theory research, one of the main goals is to design control laws which minimizes the energy of system output. More precisely, calculating the system input \(u_t\) which minimizes the cost function below where \(y_t\) is the system output.
$$\min_{u_t} ~~ J = \sum_{t=0}^{\infty}y_t^TQy_t+u_t^TRu_t$$
Solving the optimization problem above can be equivalently formulated as a stabilization or a reference tracking problem.
The system (or the plant as it is called in the control theory literature) is steered by its control terminals (actuators) which can be a valve, current source, servo motor or any other actuation medium which depends on the structure of physical system. Also, the system can have measurement terminals where sensors can be attached. The measurement can be the voltage on a capacitor, liquid level, motor speed or anything measurable in the physical system.
A fundamental open problem in the control theory is; can you stabilize the system by using a static controller?
Static controller
Dynamical systems have memory, meaning that they keep the information from the previous input. Their current output is a combination of the current and all previous input. Mathematical model of a discrete time linear time invariant (LTI) system can be written as
$$x_{t+1}=Ax_t+Bu_t, ~~~ y_t=Cx_t,$$
where \(x \in \mathbb{R}^n\) is the state vector (memory), \(u \in \mathbb{R}^m\) is the input, \(y \in \mathbb{R}^r\) is the output and \(A,~B,~C\) are matrices with proper dimensions.
Static systems are memory-less, meaning the current output depends only on the current input. Meaning,
$$y_t = Du_t.$$
Controller is placed between the plant's output and input, measuring its output and generating the appropriate input that achieves the goal of considered control problem.
One can find a dynamical controller for any system if it satisfies certain conditions (stabilizability and detectability). However, calculating a static controller is not straightforward.
A fundamental problem in the control theory literature is calculating a static output feedback (SOF) gain which achieves the control problem's goals. In mathematical terms, a SOF gain is a constant matrix (\(K\)) and the stabilizing input (\(u_t\)) at time \(t\) is the product of SOF gain and the plant's output (\(y_t\)),
$$u_t = -Ky_t.$$
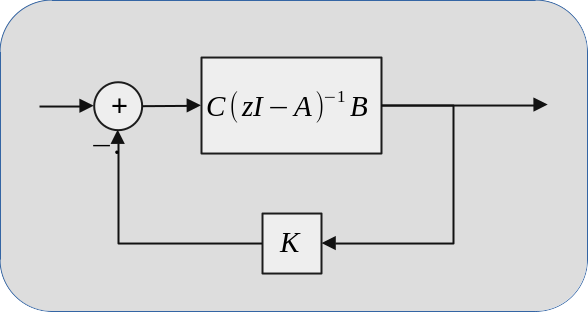
In my thesis [2] and the research article [1], optimal SOF gain calculation in terms of minimizing the total energy of the output is investigated and an algorithm which calculates SOF gains comparable to the optimal state feedback controllers is developed. One should visit the research article and Chapter 5 of the thesis for detailed explanation and analysis.
Also, you can find a Python implementation of the algorithm on this github page.
SOF algorithm as a web service
This form is an interface to use an improved version of the algorithm proposed in my thesis. You can find example problems and solutions in the links below.
Dynamically weighted LQR
Furthermore, this form is an interface to a state feedback calculator which allows to use dynamic cost function weights on the system output. The goal of linear quadratic regulator (LQR) problem is to find a state feedback gain \(F\) which minimizes the cost function
$$\sum_{t=0}^{\infty}y_t^TQy_t+u_t^TRu_t$$
when control rule is selected as \(u_t=Fx_t\). Instead of using a constant matrix \(Q\) in the cost function, one can shape the closed loop frequency response by minimizing the cost with respect to \(Q(z)y_t\) where \(Q(z)\) is a LTI transfer function. Then, the cost function becomes
$$ \sum_{t=0}^{\infty}\tilde{y}_t^T\tilde{y}_t+u_t^TRu_t, ~~\tilde{Y}(z)=Q(z)Y(z) $$
where \(Y(z)\) is the z-transform of \(y_t\).
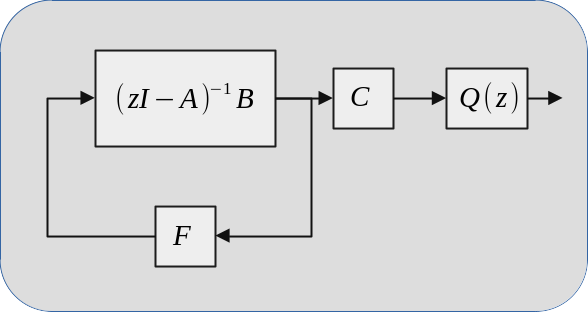
$$ Q(z) = C_q\left(zI-A_q\right)^{-1}B_q+D_q $$
Both algorithms are designed as web services, but will be made open source after completing and publishing the algorithms.